Curse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces (often with hundreds or thousands of dimensions) that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.
There are multiple phenomena referred to by this name in domains such as sampling, combinatorics, machine learning and data mining. The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data becomes sparse. This sparsity is problematic for any method that requires statistical significance. In order to obtain a statistically sound and reliable result, the amount of data you need to support the result often grows exponentially with the dimensionality. Also organizing and searching data often relies on detecting areas where objects form groups with similar properties; in high dimensional data however all objects appear to be sparse and dissimilar in many ways which prevents common data organization strategies from being efficient.
The term curse of dimensionality was coined by Richard E. Bellman when considering problems in dynamic optimization.[1][2]
The "curse of dimensionality" is often used as a blanket excuse for not dealing with high-dimensional data. However, the effects are not yet completely understood by the scientific community, and there is ongoing research. On one hand, the notion of intrinsic dimension refers to the fact that any low-dimensional data space can trivially be turned into a higher dimensional space by adding redundant (e.g. duplicate) or randomized dimensions, and in turn many high-dimensional data sets can be reduced to lower dimensional data without significant information loss. This is also reflected by the effectiveness of dimension reduction methods such as principal component analysis in many situations. For distance functions and nearest neighbor search, recent research also showed that data sets that exhibit the curse of dimensionality properties can still be processed unless there are too many irrelevant dimensions, while relevant dimensions can make some problems such as cluster analysis actually easier.[3][4] Secondly, methods such as Markov chain Monte Carlo or shared nearest neighbor methods[3] often work very well on data that was considered intractable by other methods due to its high dimensionality.
Contents |
Combinatorics
In some problems, each variable can take one of several discrete values, or the range of possible values is divided to give a finite number of possibilities. Taking the variables together, a huge number of combinations of values must be considered. This effect is also known as the combinatorial explosion. Even in the simplest case of binary variables, the number of possible combinations already is 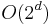 , exponential in the dimensionality. Naively, each additional dimension doubles the effort needed to try all combinations.
, exponential in the dimensionality. Naively, each additional dimension doubles the effort needed to try all combinations.
Sampling
There is an exponential increase in volume associated with adding extra dimensions to a mathematical space. For example, 100 evenly-spaced sample points suffice to sample a unit interval with no more than 0.01 distance between points; an equivalent sampling of a 10-dimensional unit hypercube with a lattice with a spacing of 0.01 between adjacent points would require 1020 sample points: thus, in some sense, the 10-dimensional hypercube can be said to be a factor of 1018 "larger" than the unit interval. This effect is a combination of the combinatorics problems above and the distance function problems explained below.
Optimization
When solving dynamic optimization problems by numerical backward induction, the objective function must be computed for each combination of values. This is a significant obstacle when the dimension of the "state variable" is large.
Machine learning
In machine learning problems that involve learning a "state-of-nature" (maybe an infinite distribution) from a finite number of data samples in a high-dimensional feature space with each feature having a number of possible values, an enormous amount of training data are required to ensure that there are several samples with each combination of values. With a fixed number of training samples, the predictive power reduces as the dimensionality increases, and this is known as the Hughes effect[5] or Hughes phenomenon (named after Gordon F. Hughes).[6][7]
Bayesian statistics
The curse of dimensionality has often been a difficulty with Bayesian statistics, for which the posterior distributions often have many parameters.
However, this problem has been largely overcome by the advent of simulation-based Bayesian inference, especially using Markov chain Monte Carlo methods, which suffices for many practical problems. Of course, simulation-based methods converge slowly and therefore simulation-based methods are not a panacea for high-dimensional problems.
Distance functions
When a measure such as a Euclidean distance is defined using many coordinates, there is little difference in the distances between different pairs of samples.
One way to illustrate the "vastness" of high-dimensional Euclidean space is to compare the proportion of a hypersphere with radius  and dimension
and dimension  , to that of a hypercube with sides of length
, to that of a hypercube with sides of length 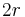 , and equivalent dimension.
, and equivalent dimension.
The volume of such a sphere is:
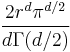
The volume of the cube would be:
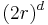
As the dimension  of the space increases, the hypersphere becomes an insignificant volume relative to that of the hypercube. This can clearly be seen by comparing the proportions as the dimension
of the space increases, the hypersphere becomes an insignificant volume relative to that of the hypercube. This can clearly be seen by comparing the proportions as the dimension  goes to infinity:
goes to infinity:
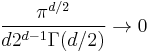 .
.
as 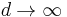 .
.
Thus, in some sense, nearly all of the high-dimensional space is "far away" from the centre, or, to put it another way, the high-dimensional unit space can be said to consist almost entirely of the "corners" of the hypercube, with almost no "middle". This is an important intuition for understanding the chi-squared distribution.
Given a single distribution, the minimum and the maximum occurring distances become indiscernible as the difference between the minimum and maximum value compared to the minimum value converges to 0:[8]
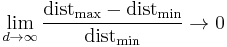 .
.
This is often cited as distance functions losing their usefulness in high dimensionality.
Nearest neighbor search
The effect complicates nearest neighbor search in high dimensional space. It is not possible to quickly reject candidates by using the difference in one coordinate as a lower bound for a distance based on all the dimensions.[9][10]
However, recent research indicates that the mere number of dimensions does not necessarily result in problems,[3] since relevant additional dimensions can also increase the contrast. In addition, the resulting ranking remains useful to discern close and far neighbors. Irrelevant ("noise") dimensions however reduce the contrast as expected. In time series analysis, where the data are inherently high-dimensional, distance functions also work reliably as long as the signal-to-noise ratio is high enough.[4]
k-nearest neighbor classification
Another effect of high dimensionality on distance functions concerns k-nearest neighbor (k-NN) graphs constructed from a data set using some distance functions. As dimensionality increases, the indegree distribution of the k-NN digraph becomes skewed to the right, resulting in the emergence of hubs, as data instances that appear in many more k-NN lists of other instances from the data set than expected. This phenomenon can have a considerable impact on various techniques for classification (including the k-NN classifier), semi-supervised learning, and clustering,[11] and it also affects information retrieval.[12]
See also
References
- ^ Richard Ernest Bellman; Rand Corporation (1957). Dynamic programming. Princeton University Press. ISBN 9780691079516. http://books.google.com/books?id=7omhQgAACAAJ.
Republished: Richard Ernest Bellman (2003). Dynamic Programming. Courier Dover Publications. ISBN 9780486428093. http://books.google.com/books?id=fyVtp3EMxasC. - ^ Richard Ernest Bellman (1961). Adaptive control processes: a guided tour. Princeton University Press. http://books.google.com/books?id=POAmAAAAMAAJ.
- ^ a b c Houle, Michael E.; Kriegel, Hans-Peter; Kröger, Peer; Schubert, Erich; Zimek, Arthur (2010). "Can Shared-Neighbor Distances Defeat the Curse of Dimensionality?" (PDF). Scientific and Statistical Database Management. Lecture Notes in Computer Science. 6187. pp. 482. doi:10.1007/978-3-642-13818-8_34. ISBN 978-3-642-13817-1. http://www.dbs.ifi.lmu.de/~zimek/publications/SSDBM2010/SNN-SSDBM2010-preprint.pdf.
- ^ a b Bernecker, Thomas; Houle, Michael E.; Kriegel, Hans-Peter; Kröger, Peer; Renz, Matthias; Schubert, Erich; Zimek, Arthur (2011). "Quality of Similarity Rankings in Time Series". Advances in Spatial and Temporal Databases. Lecture Notes in Computer Science. 6849. pp. 422. doi:10.1007/978-3-642-22922-0_25. ISBN 978-3-642-22921-3.
- ^ Oommen, T. .; Misra, D. .; Twarakavi, N. K. C.; Prakash, A. .; Sahoo, B. .; Bandopadhyay, S. . (2008). "An Objective Analysis of Support Vector Machine Based Classification for Remote Sensing". Mathematical Geosciences 40 (4): 409. doi:10.1007/s11004-008-9156-6.
- ^ Hughes, G.F., 1968. "On the mean accuracy of statistical pattern recognizers", IEEE Transactions on Information Theory, IT-14:55-63.
- ^ Not to be confused with the unrelated, but similarly named, Hughes effect in electromagnetism (named after Declan C. Hughes) which refers to an asymmetry in the hysteresis curves of laminated cores made of certain magnetic materials, such as permalloy or mu-metal, in alternating magnetic fields.
- ^ Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. (1999). "When is “Nearest Neighbor” Meaningful?". Proc. 7th International Conference on Database Theory - ICDT'99. LNCS 1540: 217–235. doi:10.1007/3-540-49257-7_15. ISBN 978-3-540-65452-0.
- ^ R. B. Marimont and M. B. Shapiro, "Nearest Neighbour Searches and the Curse of Dimensionality", Journal of the Institute of Mathematics and its Applications, 24, 1979, 59-70.
- ^ E. Chavez et al., "Searching in Metric Spaces", ACM Computing Surveys, 33, 2001, 273-321.
- ^ Radovanović, Miloš; Nanopoulos, Alexandros; Ivanović, Mirjana (2010). "Hubs in space: Popular nearest neighbors in high-dimensional data". Journal of Machine Learning Research 11: 2487–2531. http://www.jmlr.org/papers/volume11/radovanovic10a/radovanovic10a.pdf
- ^ Radovanović, M.; Nanopoulos, A.; Ivanović, M. (2010). "On the existence of obstinate results in vector space models". Proceeding of the 33rd international ACM SIGIR conference on Research and development in information retrieval - SIGIR '10. pp. 186. doi:10.1145/1835449.1835482. ISBN 9781450301534.
Further reading
- Powell, Warren B. 2007. Approximate Dynamic Programming: Solving the Curses of Dimensionality. Wiley, ISBN 0470171553.